Skip to content

Fair Chess and Simultaneous Games

The game of chess is famously flawed due to the first-move advantage, in which the player who moves first has a significant advantage. Let's fix it and make it fair.

Simultaneous Chess

Perhaps the simplest way to get rid of a first-move advantage is to remove the first move: we'll consider chess variants where both players move simultaneously. This is a well-studied concept in game theory, called a simultaneous game. We might have a setup where in each round of play:

  1. Both players write down a move in algebraic notation. I'll call this "requesting" a move.
  2. Players reveal their moves simultaneously.
  3. Their moves are both executed, possibly with some resolution of conflicts. I'll call this "merging" the moves.
Fig. 1 - Both players request Bh6; what happens?

The interesting part of designing such a simultaneous game is determining the rules for resolving merge conflicts in step 3. For example, what happens when both players move a piece to the same square? Some possibilities include:

  • Both pieces are captured.
  • Both pieces stay at their original square.
  • The higher-valued piece captures the lower-valued piece.
  • Pieces are animated one square at a time towards their destination, and the piece to arrive last captures the piece already there.
  • Players enter a boxing ring and fight for the square.

Simultaneous Games in General

All of those conflict resolution rules are fair, but I'm especially interested in rules that apply to all games. The problem with the resolutions above is that they are specific to the rules of chess. For example, they won't transfer to a game like tic-tac-toe where pieces aren't moved but rather placed.

Fig. 2 - Both players request the center square; what happens?

In particular, I want a sort of function mapping turn-based input games to simultaneous games. Without getting too formal, these input games could be defined via their game trees by providing:

  • An initial game state
  • A partial function from game states and player moves to new game states
  • A partial function from game states to winning players

It's important to note that the information about whose turn it is to move is not encoded in the game state, but rather in the player moves themselves. An implementation of these games would keep track of whose turn it is outside of the game state, like separating the chess clock's turn buttons from the chess board itself. This means that we'll have transitions out of states for all players.

Fig. 3 - Part of a game tree with transitions for multiple players out of a single state.

Given how opaque this general game interface is, there are only so many things we can do with it to build a simultaneous game. Lets start with:

Rule 1: Players may only submit moves that are legal in the input game.

This might seem like an obvious rule to avoid trivial output games, but certain simultaneous chess variants don't require this rule. Consider the following moves:

Fig. 4 - White preemptively tries to capture their own piece on f6.

White is assuming that Black will capture on f6, so White tries to "premove" to capture back on the same square. Such chess variants need to specify what happens when Black doesn't capture on f6. However, allowing moves like this is impossible in general simultaneous games because "capturing one's own piece" isn't a legal transition in the input game. It isn't in the game tree so it can't be described or requested through the opaque game interface.

Now we turn to the question of how to resolve conflicts in general. We'll stick to 2-player games for now, and generalize later. Again there are only so many things we can do, but I'll propose:

Rule 2: a. Moves are tried in both orders, and only moves that are legal in both orders are merged. b. If both moves are legal in both orders but a different game state is reached in each order, neither move is merged.

This rule again uses none of the details of the input game and instead speaks opaquely about states and moves. I'll illustrate how this rule manifests in chess with a few examples:

Fig. 5 - Pawn Collision

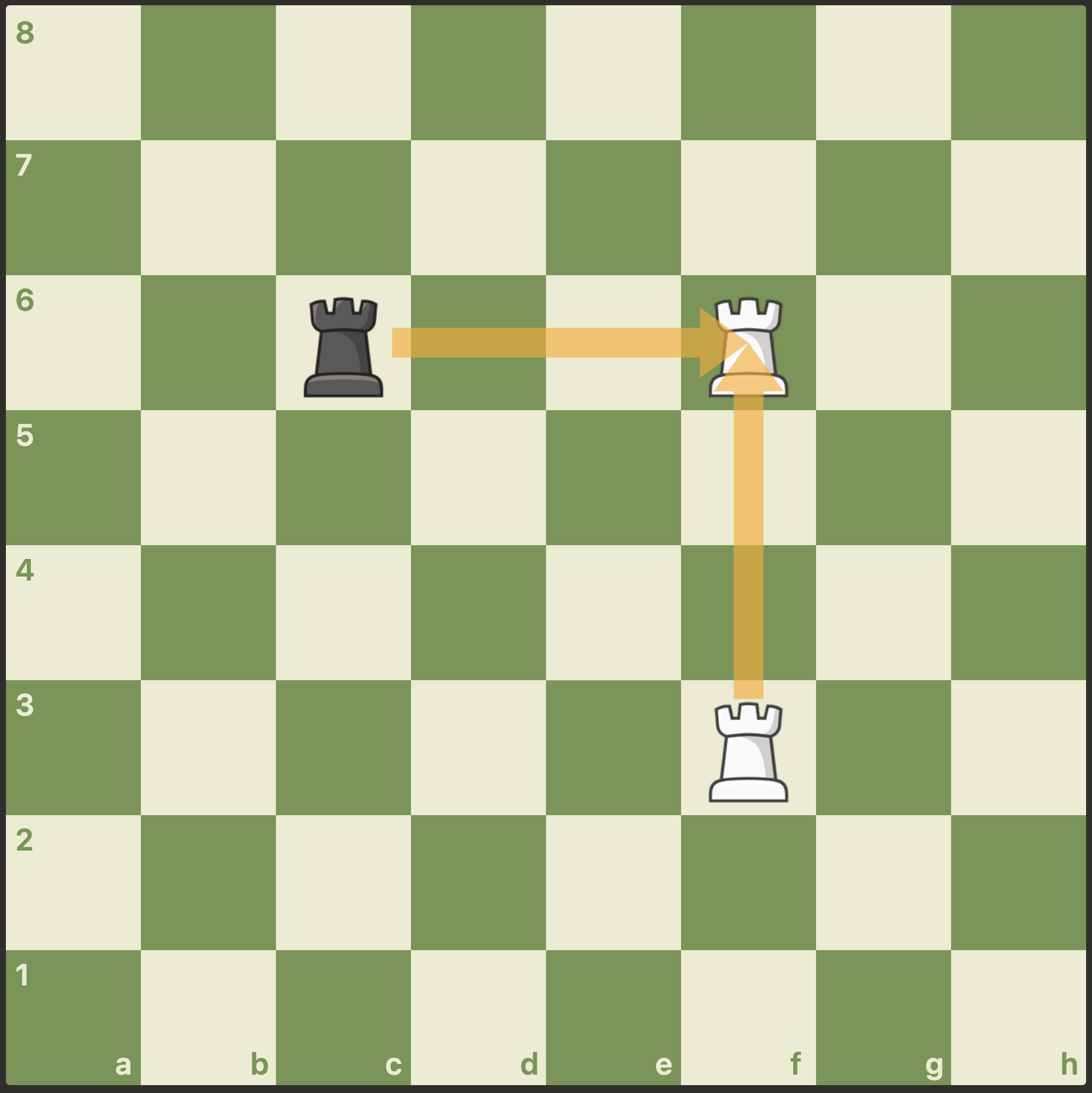
In Fig. 5, both players try e5. If White goes first, Black is blocked. If Black goes first, White is blocked. Neither move is legal in both orders, so the moves are not merged.

Fig. 6 - Rook Collision

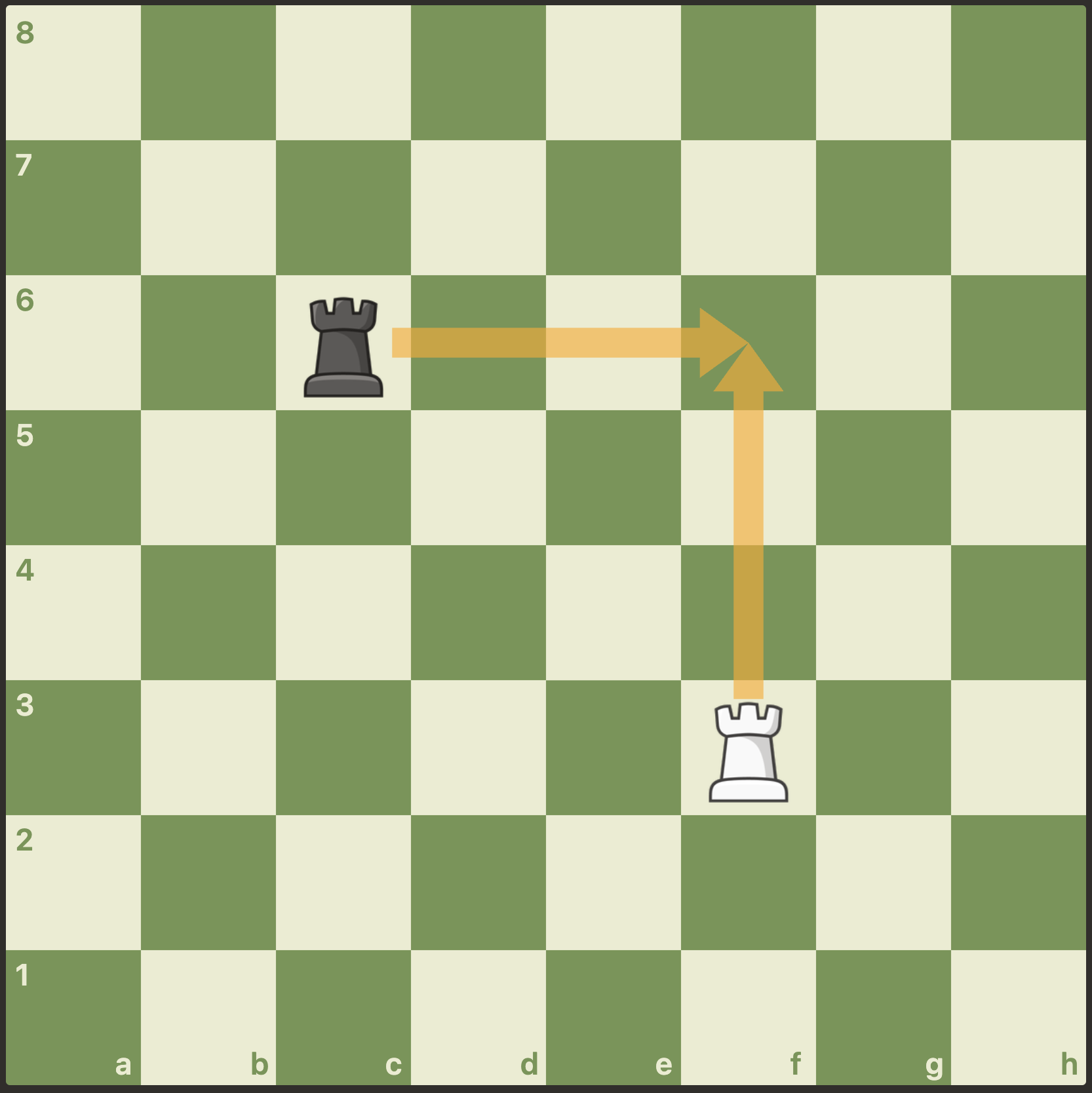
In Fig. 6, both players try Rf6. The situation is actually the same as in Fig. 5 because the moves are not Rxf6 captures, so again both moves are blocked. We could alternatively omit the capture annotation x from the definition of moves, but the result here would be the same.

Fig. 7 - Rook Block

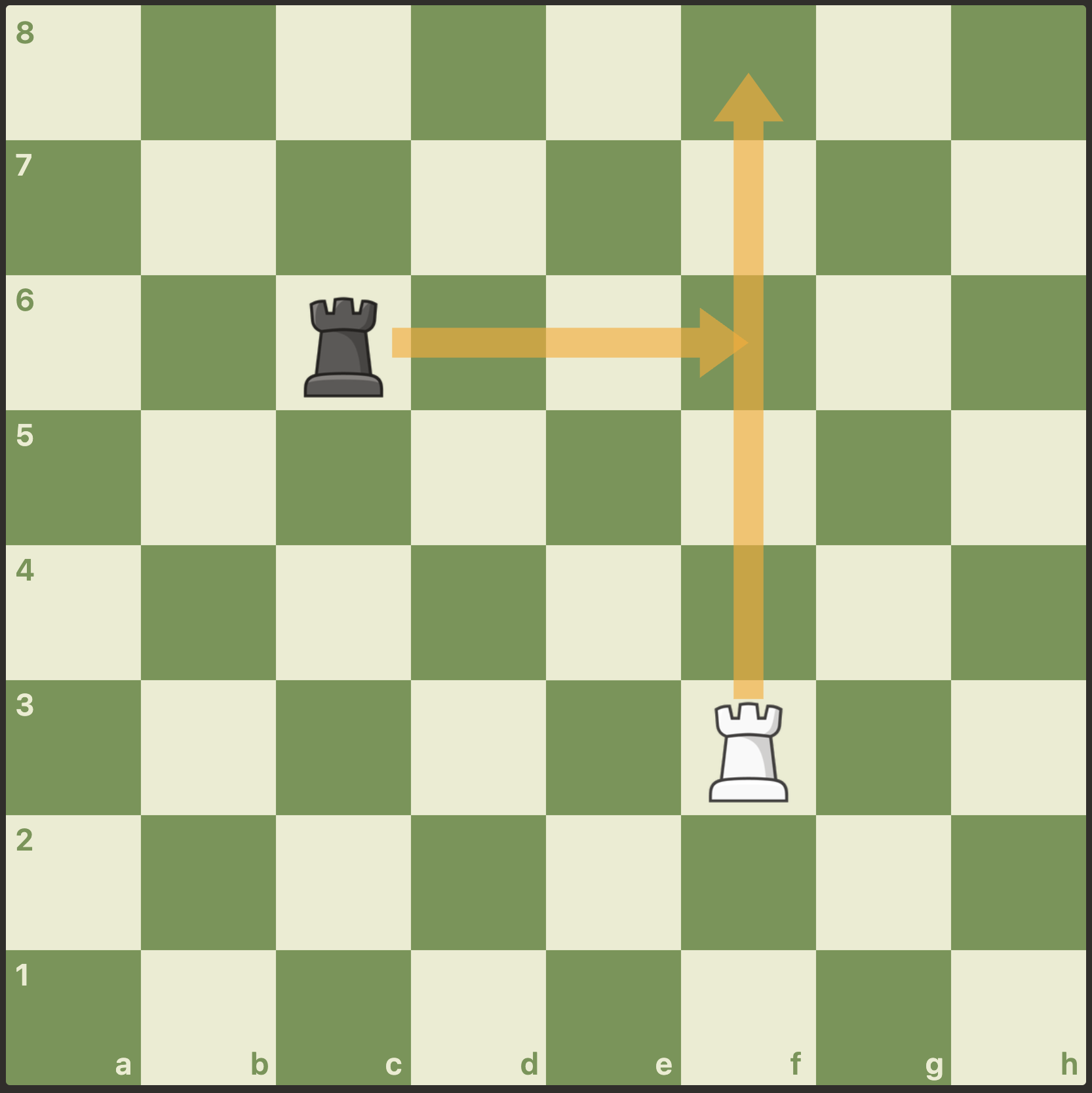
In Fig. 7, White plays Rf8 and Black plays Rf6. If White moves first, both moves are legal. If Black moves first, White is blocked. So only Black moves and White is blocked.

Fig. 8 - Rook Escape

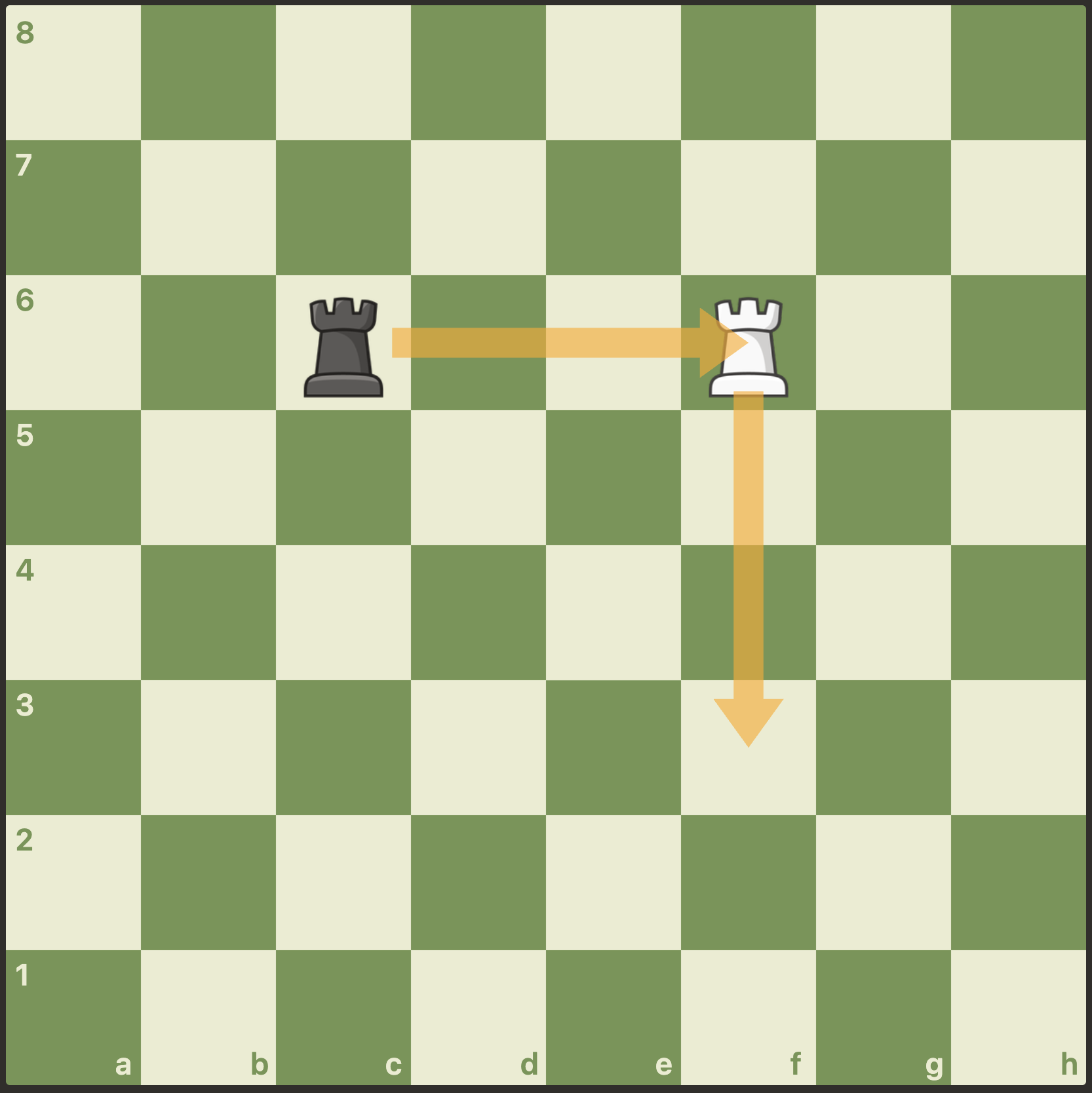
In Fig. 8, White plays Rf3 and Black plays Rxf6. If White goes first, Black's move fails because it is a capture. If Black goes first, White is captured and unable to move. Ultimately Black holds White in place and neither move is merged.

All of these scenarios illustrate rule 2a. Rule 2b is in fact irrelevant for chess, because successful moves always commute.

One might wonder what happens if two "stubborn" players repeatedly try the same rule and are both blocked. We have a couple options, including:

  • Forbid repeated moves until a successful move is made.
  • Apply a threefold repetition rule as in chess which results in a draw.
  • Do nothing and allow infinite games.

Generalizing to >2 Players

Now I'll address games with more than two players. The rules above can be easily generalized to this case by replacing "both" with "all". However with many players, this can lead to situations where very little happens, so we can do better.

In order to continue using chess examples while talking about games with more than 2 players, we'll need to modify our input game: Let each chess piece be controlled by a different player, with players split into teams based on color. Now we have 32 players, all of whom can move simultaneously! We should probably turn off friendly fire, but that's irrelevant for this discussion.

Now consider the following situation:

Fig. 9 - Three rooks and a lot of blocking.

According to our current rules, only the white rook on c5 should be allowed to move. However, the other white rook on d4 might find this unfair: c5's move should block the black rook from blocking d4's move. This is what I mean by "very little happening" in games with many players. We can make the situation even more extreme:

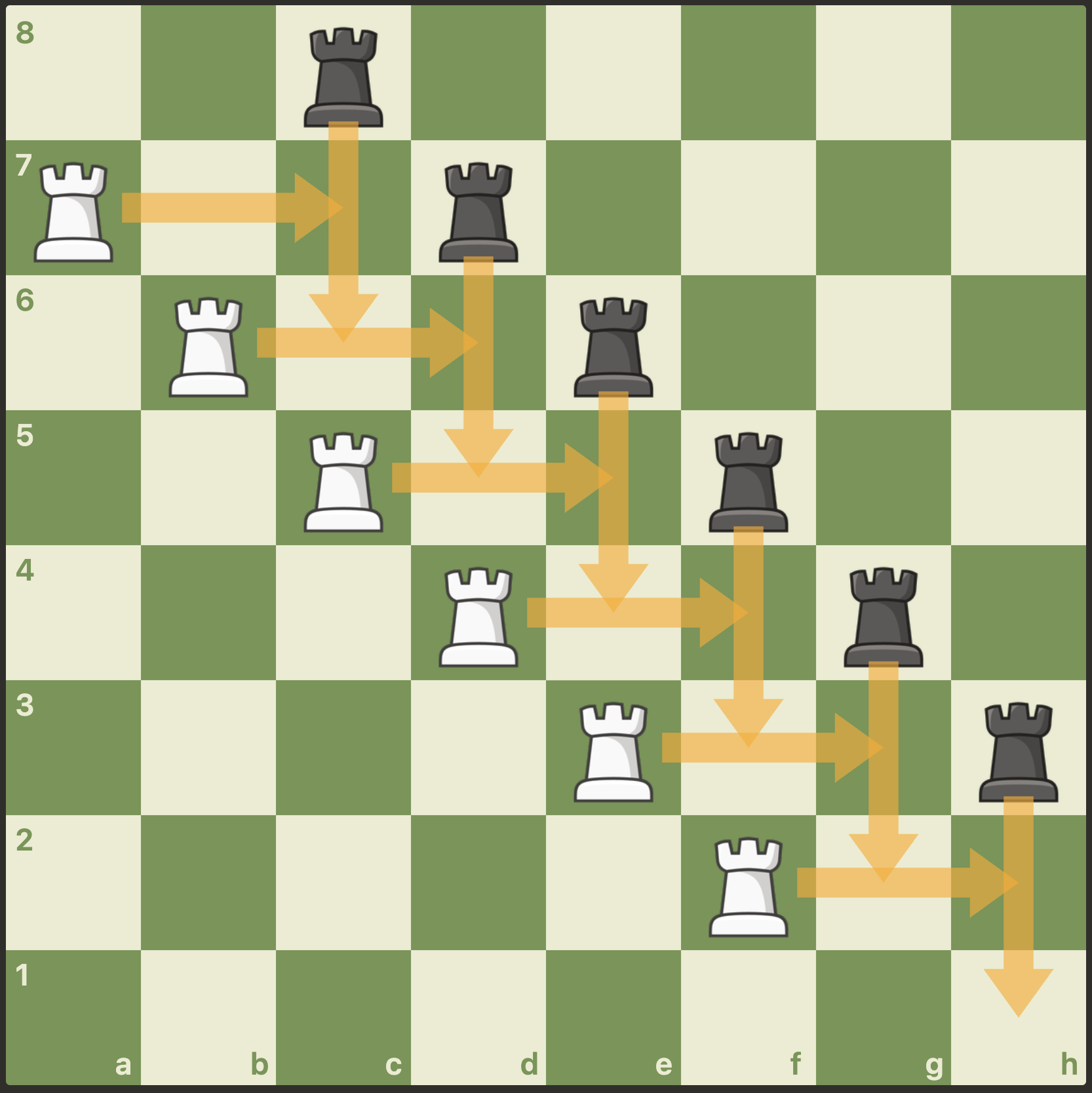
Fig. 10 - Twelve rooks and a lot of blocking.

Still only a single white rook will move in this situation. However, it seems that all of the white rooks should move because all of the black rooks are blocked. We can make this work by resolving move conflicts in the following way, which specializes to the above rules in the case of 2 players:

1 start with all moves unresolved
2 while not at fixpoint:
3     resolve all illegal moves without merging them
4     M := the set of moves legal in all orderings of unresolved moves
5     if all possible orderings of M lead to the same game state:
6         merge all moves in M and resolve them

That is, we iteratively block and merge moves until no more decisions can be made. As mentioned, when we have only 2 players, this algorithm is equivalent to the two rules above. For the case of chess and other games where legal moves commute, the check on line 5 can be omitted.

Let's apply this to the 12-rook scenario from Fig. 10.

  1. After one round of the loop, the white rook on a7 will have moved, and no other moves will be resolved.
  2. In the second round of the loop, the black rook on c8 will be blocked and resolved on line 3. This will free up the white rook on b6 to move, so M will contain just that move.
  3. In the third round of the loop, the black rook on d7 will be blocked and resolved on line 3. This will free up the white rook on c5 to move, so M will contain just that move.
  4. Ultimately, all moves will be resolved and only the white rooks will have moved.

Implementation

The computational complexity of a direct implementation of this algorithm is exponential in the worst case since we must consider all orderings of player moves. However for chess in particular, the ordering on line 4 can be handled by checking moves pairwise to compute M, and the ordering on line 5 can be handled by omitting the check altogether. This gives us a polynomial time algorithm, even on large/infinite boards where pieces might move arbitrarily far.

Edit: Mateen Kasim shared with me the counterexample to the sufficiency of checking moves pairwise in Fig. 11. Question: Is there still a polynomial time algorithm to compute M for chess? What if we fix the number of kings per team? What if we change the win condition of the input game to capturing the opponent's king, and remove checks and checkmates?

Fig. 11 - Three pairwise legal moves with an illegal ordering.

For input games where this algorithm can be implemented with constant work per player, it can be feasible to run large numbers of players in real time on a GPU. I'm working on such a game, which was the original motivation for this investigation.

Conclusion

This game we've arrived at may not the most fun simultaneous chess variant, but it makes up for quality with quantity: we have a tool to turn many classes of input games into fair simultaneous games. Some of them might turn out to be fun, but it's hard to say for sure without playtesting them.